波浪本應完美,但政、軍、經脫不了關係,必會受人為影響,石油與911恐攻是最明顯例子之一。因此波可能提早或被延後結束,川普這二年影響最明顯的是美元指數,二次都是他一句話反轉,都提早了一個月左右。美股因減稅與庫藏股而延後下跌。
如果說,對稱表現的特性是【平衡】
提供2個小技巧【關于平衡的】,供玩樂!!
1)一般的MA均線,看圖解,:

2)MACD,單位值是收盤價,不過不重要。重要的是它的特性,由於MACD使用EMA計算,權重在每個T不等。
所以,2條EMA的差值,有“歸遞”特性。由此,可以定位下一個時間點(配合結構),甚至後面幾個時間點。不精確、但是存在這現象。
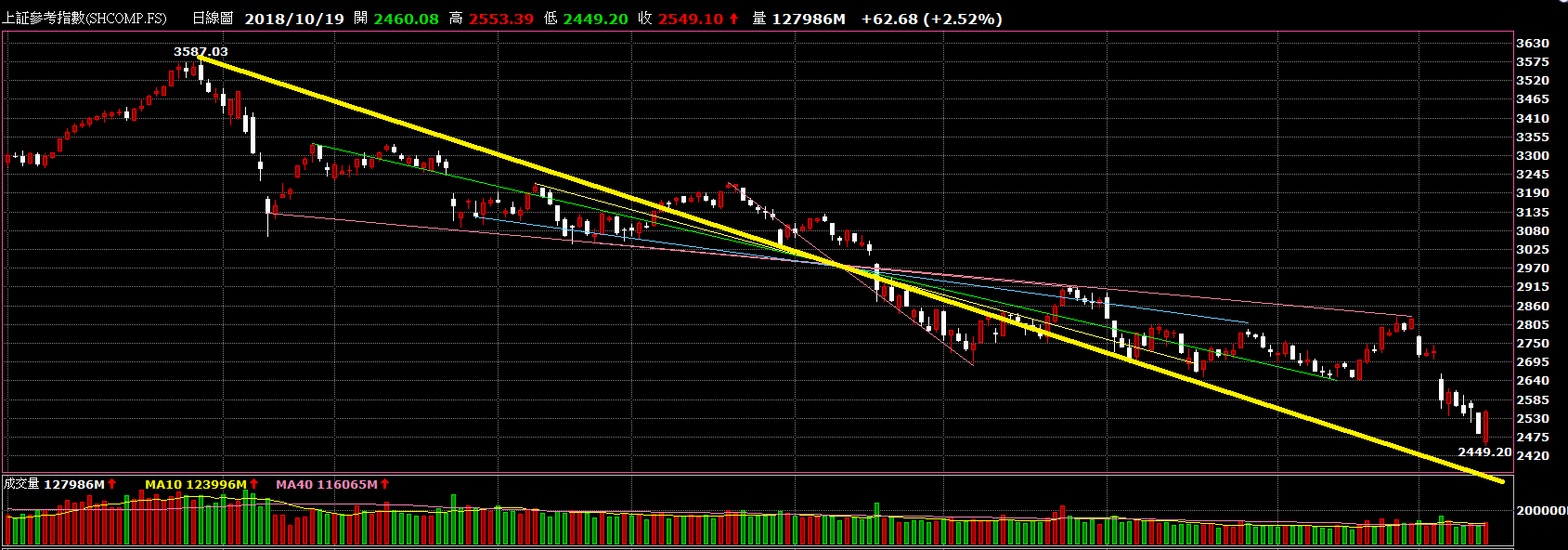
下面2張圖,第一是最近的局部,第二是較久(從3587下來)。
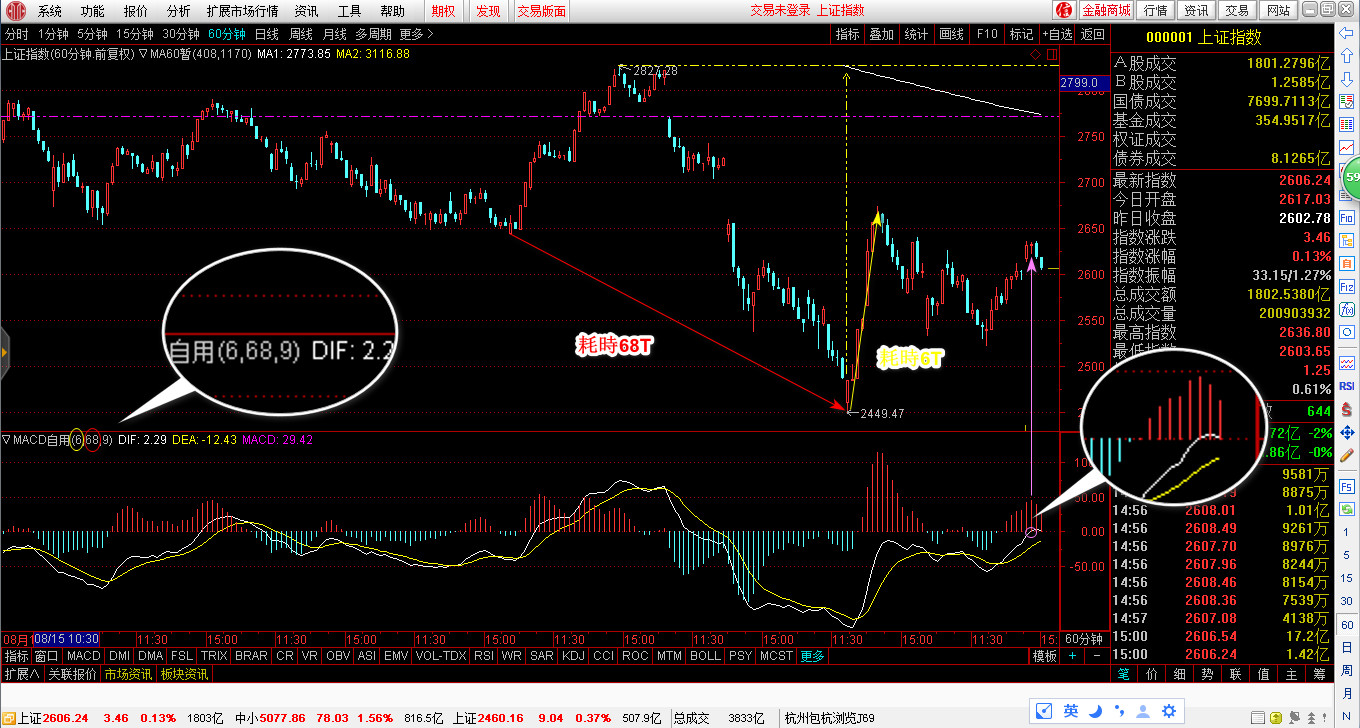

基本型態是五波,一五波在設定上是假設相等時間長與相同幅度,而第三波就由布朗運動的指數決定,有時一三五接近,且二四接近,就會有很明顯的對稱,就有明顯周期出現,用通道來看會是接近平行通道,用對稱線來看是幾乎完美,假如只要一五波相近,時間碎型不變動,都符合平行通道與對稱,但周期誤差就會變大。一旦時間碎型變動,就沒有周期可言。而這是很常見的,因為選舉而變動,因為等待某決議而變動,因為期貨決算日而變動,因此考慮周期時,可能必須考慮其他因素造成的時間延遲或提前,之後的波動,也會因為這個提早或延遲而受影響。就碎型的角度而言,周期很難穩定存在,時間越長就越難,除非如您所做的短期間,可儘量避開。所以我的預估跟您一樣,用約略相近。在小時線來看,誤差是小時,在月K線來看是幾個月。我很少做小時的碎型,因為還沒做完,那波可能結束了.......,我比較著重在大規模,抓長期趨勢。短線我用波浪約略估計波數,標準差抓支撐壓力,空頭不看撐,多頭不看壓,因為趨勢之下必破,直到遠超出倍數極限才會反彈或修正。如台股十月的支撐二個都破了,一直跌到極限值9902之外,一直到十月最後一天才快速反彈收9802。剛好30號買多單,也許明天多單就會出場。不過外資硬是壓到最後一天才放手,讓人覺得太超過了,雖然不是第一次,但並不多見。小時線我現在少用了,因為台積電的關係,一檔佔權值近20%的股票,會讓指數的波動不正常,或許是我模型需要修正,將台積電的比重列入算式,不過目前還沒空去考慮這件事,目前著重在複合波與碎型的研究中。
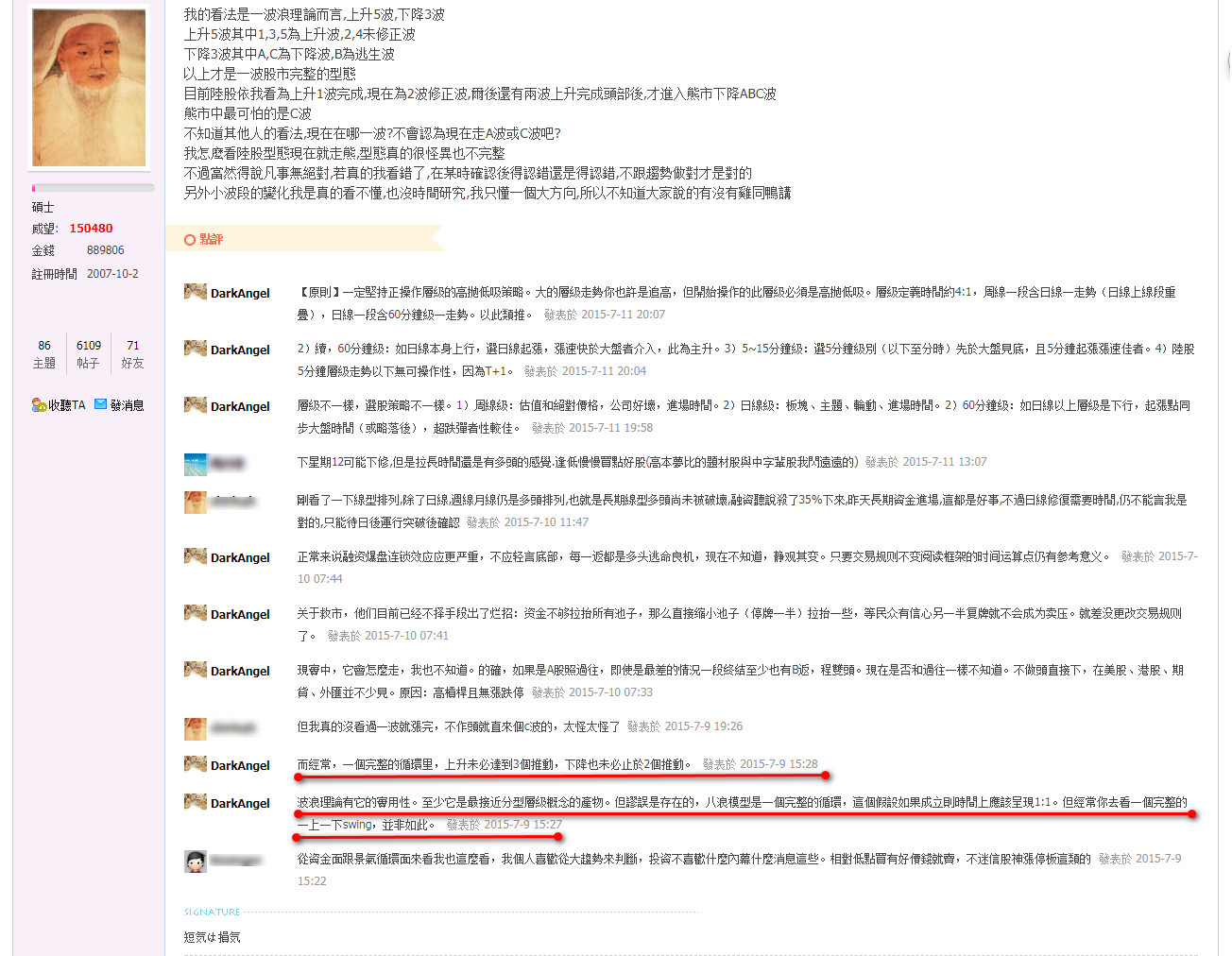
1)實際上,分型布朗運動比波浪理論更適合作為重點、更接近市場“分類”的真相。波浪理論是一種理想化、未經數據檢驗的不完整理論。(畢竟Elliot那個時代,根本就沒有數據驗證這個概念,他自己也沒憑這個賺過錢)
波浪理論最有價值就是概念中提出了層級嵌套這個概念。近似分型級別的嵌套。(不知是否誤打誤撞)
關於波浪曾經提到過的一點看法,以及市場近似分型(分數)布朗運動:

2)週期其實是一種“幻象”,只是現象不是原理。但說到形、數、理、象,它是可以連續性去描述市場狀態的一種觀測標尺。
如果,已經建立算法,讓電腦自己去耦合(擬合)特徵,取得概率分佈。當然就不需要去計算週期。但是就投入交易使用來說,完全照算法建模對硬體要求太高,有時效性問題。近似傳統的技術分析方式反而更有指導作用(前提是,經過大量數據檢測過傳統技術分析的一些假設是否存在、被證實。)
3)週期這種幻象,其實一直都存在。若投入使用,難的其實在於怎麽正確採樣(時間序列可能出現無數種樣本、分型也可能無數種,怎麽去選最能解決當下問題的)。但是非常有用,尤其是對數週期冪率模型(LPPL模型,冪法則和正向回饋),可以說是神一般的模型。對於超指數型增長、衰竭數據,臨界點無一缺漏。
LPPL模型,當時在2015年上證股災時,先驗性的提示:
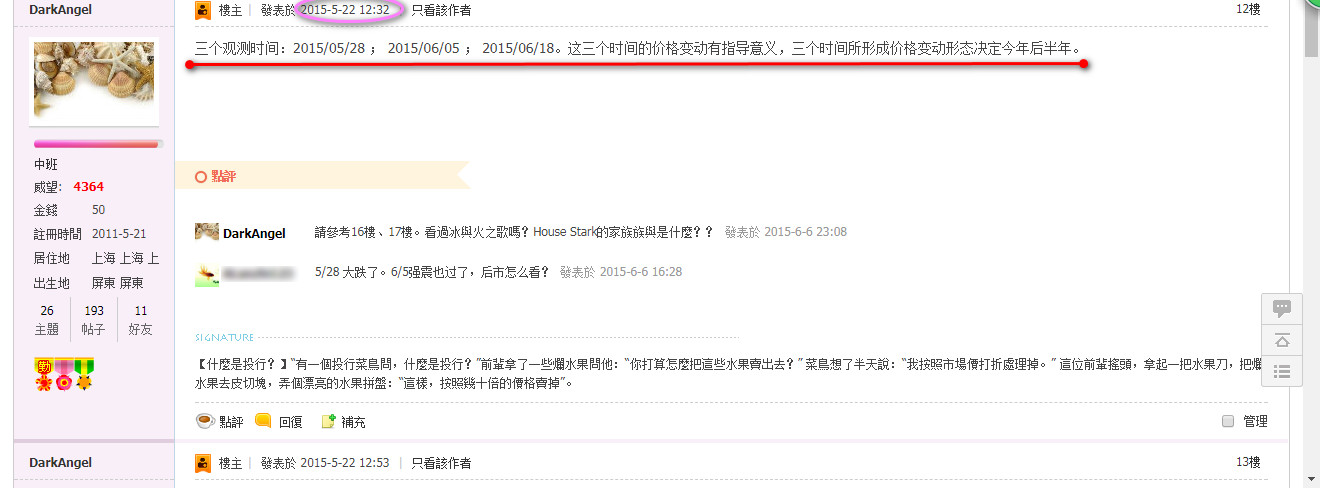
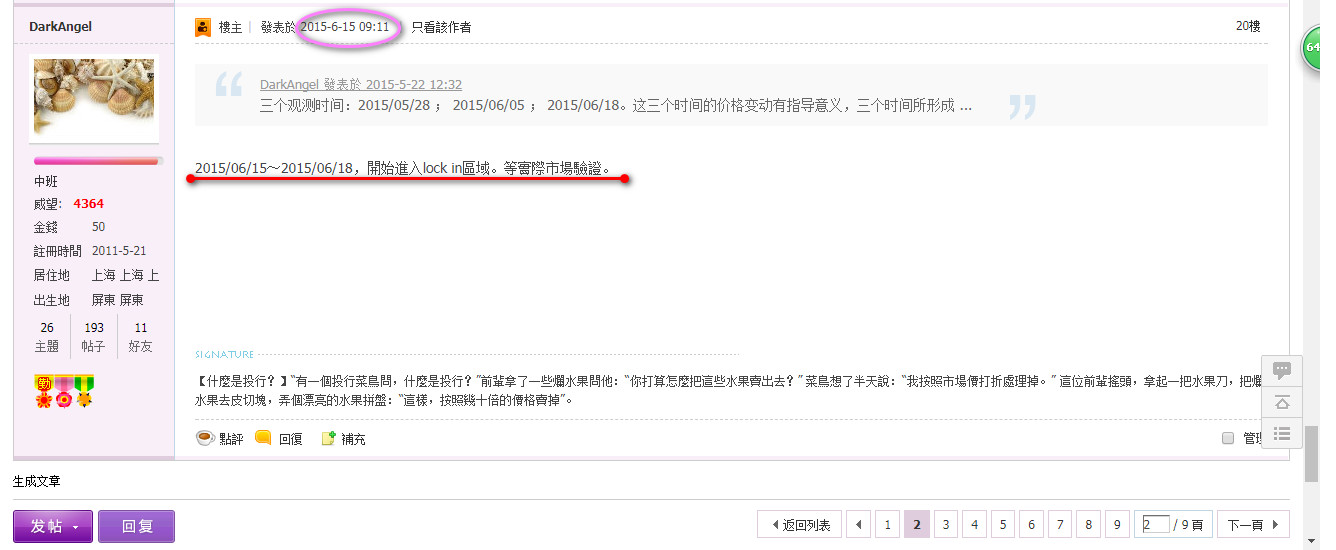

PS. ETH實驗室,之後對上證(2015/06/15,5178.19開始的崩盤),所做的有關LPPL模型的詳盡報告(
Real-Time Prediction and Post-Mortem Analysis of the Shanghai 2015 Stock Market Bubble and Crash):
http://tasmania.ethz.ch/pubfco/fco.html
LPPL的觀察站,可以比對他給的反轉訊號,很方便。他的計算總比我們來的正確太多。結果可以參考參考。紅點很多,綠點也很多,都是可能的反轉點。
ETH他們的每月報告有定期收録。但觀察上證的話,因為種種不可描述之原因,2015之後ETH很少在披露有關CH(包含上證)的觀察結果,所以只能自己算。(之前大陸市場觀察,主要是由華東理工大學教授周煒星做的,之前他師從Didier Sornette)
這模型有點nasty,因為參數7個,很難找到最優。原作者(Pro. Didier Sornette)採用的是禁忌搜索。但是依然很麻煩。網上倒是有流傳網友使用Python寫的源碼,是採用遺傳算法。(
https://uqer.io/v3/community/share/567a4fbd228e5b344568810f)
以下供參考,望有幫助:
康奈爾大學收録-
關於Pro. Sornette 論文:
[url]https://arxiv.org/find/q-fin/1/au:+Sornette_D/0/1/0/all/0/1[/url]關於zhou_W(周煒星)論文:
https://arxiv.org/find/q-fin/1/au:+Zhou_W/0/1/0/all/0/1
Sornette在TED的演講:
How we can predict the next financial crisis(我们如何预测下一场金融危机?)
LPPL有它的侷限性:能測算的數據主要需有2特徵:一是,超指數增長或衰竭;二是,時間線性尺度下,頻率不斷加速(臨界附近呈現接近“共振”狀態),對數尺度下程常數(近似“等週期”);
可以說LPPL在學術上的貢獻是第一次在計量(定量、量化上)角度,給了“泡沫”以及“反向泡沫”(Anti-Bubble)明確的定義,并提供數字上可供測量的尺度,標註出基礎物理特徵。
但是非超指數狀態下的數據,就不能使用LPPL來處理了(沒優勢),一般使用模式識別類的(比如HMM模型),或者各種動量算法,或基於統計學的概率分佈算法(交易角度上來說,還更有用)。













 SSRN-id2647354.pdf (1.56 MB)
SSRN-id2647354.pdf (1.56 MB)